The physics of a bicycle accident

Now it happened. After about 1,700 km on the bike this year, I had an accident. In Kuchl (in most beautiful Salzburg, Austria), I did a relatively sharp turn on starting when the front wheel came onto a patch of gravel. It looked most unsuspicious, but it gave way, the bike slid away sideways, and I fell to the side with almost no forward speed. Unfortunately, I was not able to get my leg out to counter the fall. Fortunately, I impacted the ground practically at the same instance with the entirety of my left forearm and the left hip. If this hadn’t been the case and the potential turned kinetic energy hadn’t been spread out, it would have been entirely possible to find myself in the hospital with something fractured. Instead, a miniscule bruise near the elbow and some minor pain around the greater trochanter (for the anatomists) on climbing stairs for a week was all. Could have been much worse. But still I wonder why I was not able to react properly even though I definitely can remember falling. How much time was it? Half a second, one second? Probably not much longer. Let’s find out.

First, I thought a free fall model could be suitable approximation. Here is the equation:

$s = \dfrac{gt^2}{2}$

With the gravitational acceleration

$g=9.8 \ ms^{-1}$

and s as the distance. I took my hip as the point of interest, which measures 1.07 m above ground when sitting on my bike. Simply solving for t should do the trick. (For more on gravitation see my Explainer right here.)

Except it doesn’t. Something didn’t feel right from the start. Think of a pencil balanced upright. On tipping over, it typically does so quite rapidly. But sometimes it can appear a bit more undecided first and only then it falls. In contrast to free fall where the gravitational acceleration enforces the way down immediately, without the tiniest delay.

We need a better model. I thought a bit. Then I had the answer. The pencil gave the clue. We can model me crashing with the bike as a pendulum.

Pendulum equation

You may have heard that a pendulum is modelled with a second-order differential equation. Sure, we could look it up. But it is much more fun to derive it from first principles.

Here is the general setup of a pendulum. (The more upright variant is just an extension of the concept.)

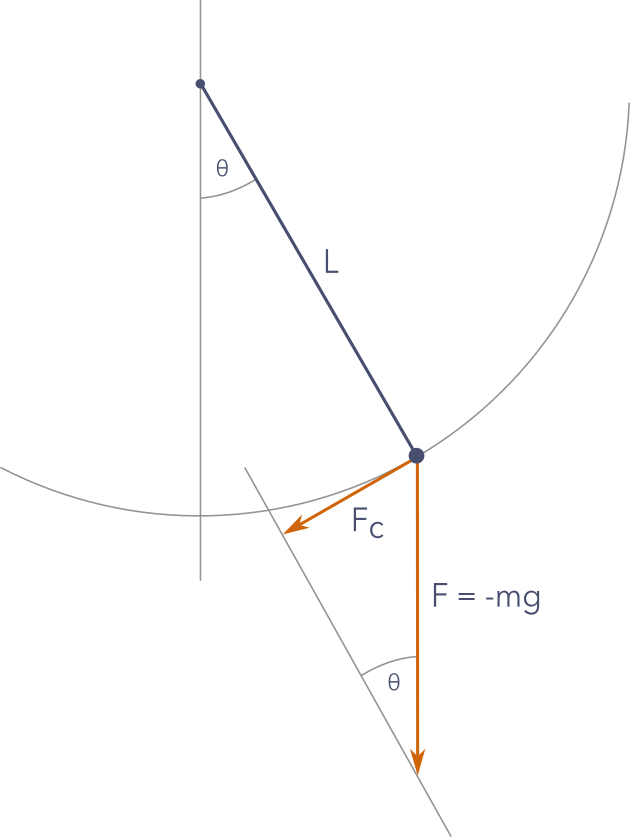
The mass m of the pendulum bob (we assume the rod to be massless) experiences the gravitational pull straight downward with

$F=-mg$

As the pendulum is affixed to the pivot point it can only move along a circular trajectory with the length of the rod L being the radius of this circle. Therefore, the gravitational force F can only impart the component force F_c on the pendulum, which we need to determine by way of a bit of trigonometry. θ (theta) is the angle between the rod and the vertical. (As we are dealing with similar triangles here the angle θ between rod and vertical is the same as the θ in the force triangle.)

$sin \theta = \dfrac{F_c}{-mg}$

$F_c = -mg \ sin \theta$

With that we have the gravitational force acting on the pendulum. At the same time we know Newton’s second law of motion:

$F = ma$

m is the mass of the pendulum here. Could we somehow get an expression for the acceleration a? For this we need the arc length formulas:

$s = \theta L$

s is the arc length for a given angle θ and a radius (that we call L for our purposes here as noted above). Please appreciate that this equation is basically the same as the formula for the circumference c of a full circle (where the angle θ happens to be 360 degrees or 2π radians).

$c = 2 \pi r$

Now it is time to remember that distances and accelerations are always tightly connected: The first derivative of distance s is velocity v, and velocity’s first derivative is acceleration a (= the second derivate of distance). Therefore:

$s = L \theta$

$v = \dfrac{ds}{dt} = L \dfrac{d \theta}{dt}$

$a = \dfrac{d^2s}{dt^2} = L \dfrac{d^2 \theta}{dt^2}$

The crucial conceptual step is that we express the change of distance with change of the angle, which is fine as the only other parameter, the rod length L is a constant.

As the bob of the pendulum can only move along the arc dictated by the rod length L, we can happily plug our newly found expression for the acceleration into Newton’s second law:

$F = ma$

$F = m L \dfrac{d^2 \theta}{dt^2}$

As this is simply another expression for the force the pendulum experiences along its trajectory, we can combine what we know:

$m L \dfrac{d^2 \theta}{dt^2} = -mg \ sin \theta$

We have m on both sides so we can cancel it. (Yes, the mass of the pendulum does not matter.)

$L \dfrac{d^2 \theta}{dt^2} = -g \ sin \theta$

Bring around the L:

$\dfrac{d^2 \theta}{dt^2} = - \dfrac{g}{L} \ sin \theta$

And this is it: the pendulum equation derived step by step. A classical second-order differential equation. What does it mean in words? The angular acceleration is proportional to the sine of the angle. Which makes good practical sense when thinking about different angles. At an angle of 0, we have sin(0)=0, at 90 °=π/2 rad we have sin(π/2)=1, and at 180 °=π rad we have sin(π)=0. The acceleration is 0 when the pendulum points straight down or straight up, and reaches its maximum when the pendulum points at a right angle to the side.

Solving the differential equation

Having a differential equation is nice and well, but we need to solve it to get meaningful results. Some differential equations can be solved analytically, most are tractable only using numerical methods. The latter approach always works, so we will use it here. From the multiple ways to do this we implement the procedure in Python.

Wait you say. The solver algorithms in Python can only handle first-order differential equation whereas we have a second-order DE here. What could we possibly do?

What we do is decomposing the second-order differential equation into a system of two first-order differential equations. Sounds more difficult than it is. And the hints for how to do this have already been alluded to above when we derived the pendulum equation as we made the connections between distance, velocity and acceleration. Here is the pendulum equation again:

$\dfrac{d^2 \theta}{dt^2} = - \dfrac{g}{L} \ sin \theta$

To express acceleration, instead of the second derivative of the angle θ, we can equivalently use the first derivative of angular velocity ω (omega):

$\dfrac{d \omega}{dt} = - \dfrac{g}{L} \ sin \theta$

And what is the first derivative of the angle θ? It is the angular velocity ω:

$\dfrac{d \theta}{dt} = \omega$

This is it. The last two first-order differential equations fully represent the second-order differential equation we started with.

Time for some coding. (I won’t go into the details of how to implement this script as I plan to bring out a kind of differential equation solving manual in its own right soon. (I will add a link here.)) One additional assumption is needed: If I chose to fall from my bike from exactly upright, I would stay there forever in this model. (We have seen above that at an angle of exactly 180 °=π rad the acceleration is 0, and without acceleration there is no movement.) A bit of ‘lean-in’ is necessary. I use 10 ° from the vertical.

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp

L = 1.07
t_span = [0, 2]
degrees = 10
theta0 = np.pi - degrees*np.pi/180  # The initial value of the angle.
omega0 = 0                          # The initial value of the velocity.

def P1(t, init):
    theta, omega = init
    d_theta = omega
    d_omgea = -9.81*np.sin(theta)/L
    return d_theta, d_omgea 

sol = solve_ivp(P1, t_span, [theta0, omega0], t_eval=np.linspace(*t_span, 1000))

# Filtering the trajectory until ground impact which happens at 90 °=pi/2 rad from the vertical.

sol_filtered = sol.y[0][sol.y[0] > np.pi/2]
t_filtered = sol.t[sol.y[0] > np.pi/2]

print(f'Time to impact: {t_filtered[-1]:.2f} s')

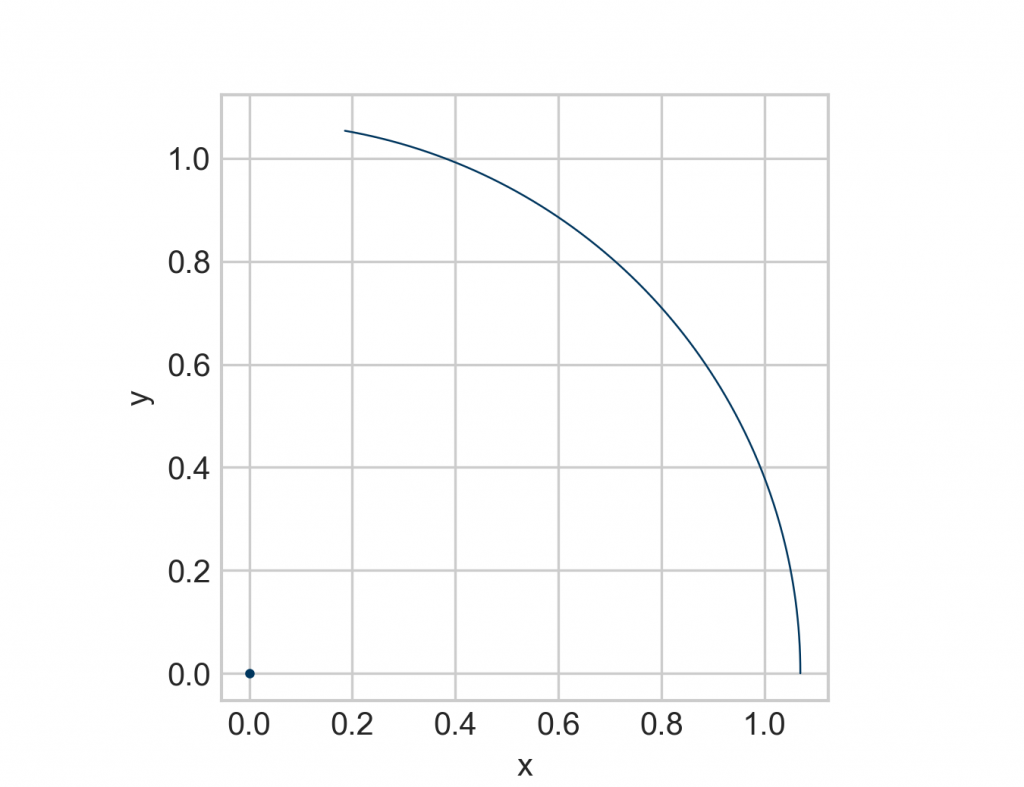
# To plot the orbit we have to calculate the x and y coordinates from the angle theta.
# Note that in a standard coordinate system, an angle of 0 coincides with the positive x axis.
# In our physical system here, theta=0 shall be the negative y axis. Therefore, we have
# to rotate the angle.

rot = sol_filtered - np.pi/2

x = np.cos(rot)*l
y = np.sin(rot)*l

plt.plot(x, y)
plt.scatter(0, 0)
plt.axis('square')
plt.xlabel('x')
plt.ylabel('y')
plt.show()

Time to impact: 0.97 s

And if you wondered what the speed was at impact, only a few additional steps are necessary. One of our system variables was angular velocity ω. We filter it from the solution vector as before and take the last item of the sequence:

omega_filtered = sol.y[0][sol.y[0] > np.pi/2]
omega_filtered[-1]

1.570857437870895

This is the angular velocity ω in radians per second. We just have to convert this into meters per second. To do that consider that angular velocity is defined as thus (with f being the frequency (with the unit s^-1):

$\omega = 2 \pi f$

Rearranged for f:

$f = \dfrac{\omega}{2 \pi}$

Insert the result from above:

$f = \dfrac{1.57}{2 \pi} = 0.25 \ s^{-1}$

The tangential velocity is (with c being the circumference of the circle here):

$v = cf = 2 \pi L f = 2 \pi \cdot 1.07 \cdot 0.25 = 1.68 \ ms^{-1}$

Or:

$v = 1.68 \cdot 3.6 = 6.05 \ kmh^{-1}$

In conclusion

It took me approximately 1 second from losing my balance to impacting the ground. Enough to experience the event in real time, but simply too short to react.

Back matter

Cite as: Gamsjäger T. The physics of a bicycle accident. Maytensor 2025

Featured image: My trusty helmet. I never go out for a ride without it. Never.

The physics of a bicycle accident

Pendulum equation

Solving the differential equation

In conclusion

Further reading

Back matter

Leave a Reply Cancel reply